 Блок схемы процесса
Блок схемы процесса
 Типы блок-схем
Типы блок-схем
 Этап 2: Текущая ситуация
Этап 2: Текущая ситуация
 Этап 3: Анализ
Этап 3: Анализ
Блок схемы процесса
Что такое блок-схема процесса?
Блок-схема - это графическое
отображение процесса, которое четко показывает нам, как протекает
процесс. Блок-схема показывает систематическую последовательность
этапов выполнения работы и то, какие группы вовлечены в процесс.
Для чего используют блок-схемы?
-
Документировать и
описывать текущий процесс.
-
Разрабатывать модификации
к текущему процессу или исследовать то, где могут возникнуть проблемы.
-
Разрабатывать совершенно
новый процесс.
-
Определять как, когда
и где, измерять текущий процесс, чтобы убедиться, соответствует
ли он устойчивым требованиям.
Типы блок-схем
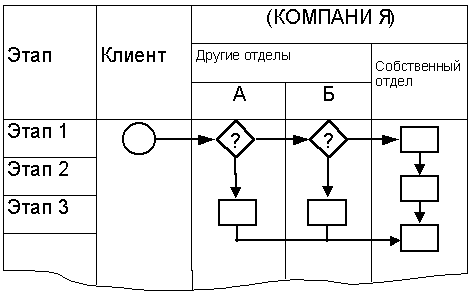
Блок схема макро уровня:
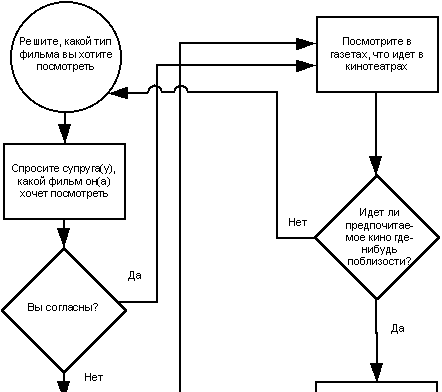
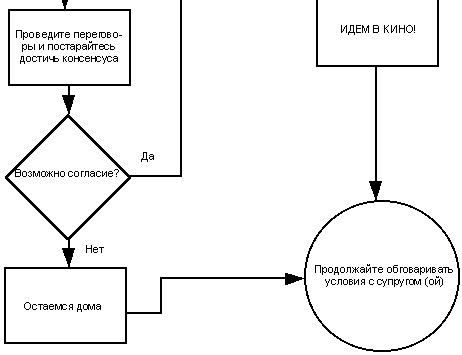
Рассмотрим блок-схему микроуровня:
"Идем в кино"
Как построить блок-схему?
Блок-схема процесса представляет
собой планирование этапов по завершению работы. Для того, чтобы
показать определенные виды деятельности, используются особые символы:
|
Круг
|
Прямоугольник
|
Ромб
|
Стрелка
|
|

|

|

|
|
|
Начальный и конечный
этапы
|
Этапы, виды деятельности
внутри процесса
|
Ситуации, требующие
принятия решения
|
Направление от
одного деятельности к другому
|
Можно использовать символы
в виде точек, чтобы показать второстепенное направление процесса
(пример: копия используемого бланка возвращается к разработчику).
Первый ряд используется
для того, чтобы разделить процесс на сферы ответственности.
Первая колонка используется
для того, чтобы определить общие этапы и их продолжительность.
Этапы должны быть организованы
так, чтобы каждый этап попадал в нужную сферу ответственности.
Когда использовать блок-схемы?
Блок-схема процесса требуется
в этапах "Текущая ситуация" и "Стандартизация";
однако, блок-схемы также можно использовать в этапах "Основания
для улучшения", "Анализ", "Контрмеры"
Этап 2: Текущая ситуация
Цель - выбрать проблему
и определить задачу для улучшения.
Деятельность
-
Соберите данные по
всем аспектам вашей области.
-
Определите устойчивые
требования потребителей.
-
Напишите четкое определение
проблемы.
-
Примените данные
для постановки задачи.
Полезные приемы / средства
-
Контрольный листок
-
Гистограмма
-
Парето диаграмма
-
Контрольная диаграмма
-
График
Примеры:
|
График Парето
|
График
|
|
|
|
Гистограмма
Что такое гистограмма?
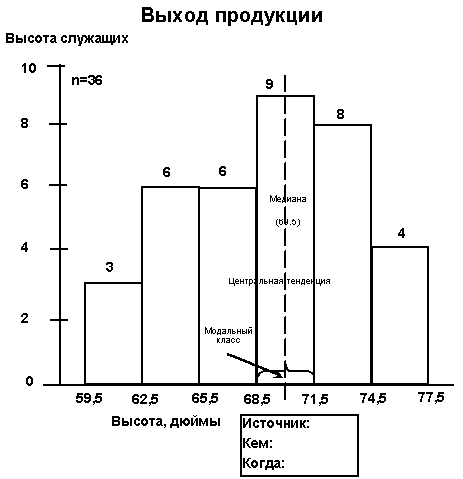
Гистограмма, которую также
называют распределением частот, - это визуальное изображение распределения
данных (например, рост 36 служащих в дюймах). Информация на гистограмме
изображается с помощью серии прямоугольников или полос одинаковой
ширины. Высота этих полос указывает количество данных в каждом классе.
Частотность событий указывается
по вертикальной оси, а группа данных, или классы, указываются по
горизонтальной оси. Чтобы провести оценку гистограммы, мы должны
знать центральную тенденцию, а также рассеивание данных.
Измерение центральной тенденции
-
Середина (среднее
значение) - сумма всех измеренных или подсчитанных данных, разделенная
на общее количество данных; например, складываем все данные, получаем
2482, делим на 36 и получаем 68.9 дюймов.
-
Значение, наиболее
часто повторяющееся в необработанных данных. В нашем примере это
70 дюймов. Если данные представлены в виде групповой частотности,
то мы говорим о модальном классе. Модальный класс - это интервал
с наиболее высокой частотностью. В данном примере модальный класс
составляет 68.5 - 71.5.
-
Медиана - середина
всех измеренных или подсчитанных данных (если четное количество
данных, то медиана будет дробной); например, в нашем примере с 36
измерениями значением медианы является среднее значение тех измерений,
которые находятся в середине (69+70=139, делим на 2, получаем 69.5
дюймов).
Измерение рассеивания
-
Диапазон - максимальное
значение минус минимальное значение.
-
Стандартное отклонение
(СО) - измерение, которое показывает на сколько широко рассеялся
какой-то набор данных от середины. К стандартному отклонению относятся
все данные. Оно намного менее восприимчиво к добавлению других данных,
чем диапазон, и поэтому, это более надежный способ измерения отклонения.
Рассмотрим пример построения
гистограммы "Высота служащих"
|
Служащий
|
высота (дюйм)
|
Служащий
|
высота (дюйм)
|
Служащий
|
высота
(дюйм)
|
|
ТК
|
64
|
СТ
|
69
|
ШП
|
68
|
|
ВШ
|
63
|
РМ
|
71
|
РС
|
72
|
|
ТК
|
66
|
СТ
|
73
|
ШП
|
75
|
|
ВШ
|
73
|
РМ
|
62
|
РС
|
76
|
|
ТК
|
60
|
СТ
|
70
|
ШП
|
69
|
|
ВШ
|
67
|
РМ
|
65
|
РС
|
70
|
|
ТК
|
68
|
СТ
|
72
|
ШП
|
72
|
|
ВШ
|
70
|
РМ
|
63
|
РС
|
70
|
|
ТК
|
65
|
СТ
|
73
|
ШП
|
76
|
|
ВШ
|
61
|
РМ
|
74
|
РС
|
73
|
|
ТК
|
66
|
СТ
|
70
|
ШП
|
65
|
|
ВШ
|
76
|
РМ
|
66
|
РС
|
69
|
Чем полезна гистограмма?
Не всегда легко просмотреть
измеренные данные и определить образцы или проанализировать то,
что нам сообщают эти данные. Гистограмма может предоставить информацию
о степени разнородности данных и указать образец распределения.
Рисуя кривую линию по верхушкам полосок гистограммы, мы можем получить
общую картину.
Рассеивание данных может
привести к большому разнообразию гистограмм, в зависимости от того
процесса или объекта, по которому вы собрали данные. Далее предлагаются
некоторые типичные виды гистограмм.
Виды гистограмм
-
Симметричная (пример
А)
Большинство значений
находятся по обе стороны от центра распределения (центральной тенденции)
с отклонением, сбалансированным по обе стороны от центра.
-
С наклоном (пример
Б)
Большинство значений находятся слева от центральной тенденции. Такой тип
распределения данных может произойти, если есть естественное препятствие,
или в случаях сортировки данных (товары, которые не соответствуют
определенному стандарту, удаляются из набора данных).
-
Асимметричная (пример
В)
На таком графике имеется длинный "хвост" по одну сторону от
центральной тенденции. По одну сторону имеется больше отклонений,
чем по другую, указывая на то, что в течение процесса произошел
сдвиг некоторых переменных значений.
-
Двухмодальная (пример
Г)
В двух модальном типе имеется две вершины. Это обычно происходит, когда
смешиваются две различные группы данных (категория невысоких людей
смешивается с категорией очень высоких людей). В действительности,
мы имеем две гистограммы, объединенные вместе.
Как построить гистограмму?
Чтобы построить гистограмму,
нарисуйте горизонтальную и вертикальную оси. Горизонтальная ось
(Х) отображает интервалы; вертикальная ось (Y), отображает частоты.
Нарисуйте полоску, представляющую собой частотность данных в каждом
классе. Полоски должны соприкасаться друг с другом.
Последовательность действий приведена
в таблице.
| Этап |
Уравнение |
Пример |
| Начните
с неорганизованного набора, по крайней мере, 30 данных
|
|
64,
63, 66, 73, 60, 67, 68, 70, 65, 61, 66, 76, 69, 71, 73, 62,
70, 65, 72, 63, 73, 74, 70, 66, 68, 72, 75, 76, 69, 70, 72,
70, 76, 73, 65, 69 |
| Расставьте
цифры в нисходящем или в восходящем порядке. |
|
60,
61, 62, 63, 63, 64, 65, 65, 65, 66, 66, 66, 67, 68, 68, 69,
69, 69, 70, 70, 70, 70, 70, 71, 72, 72, 72, 73, 73, 73, 73,
74, 75, 76, 76, 76 |
| Каждая
цифра является единицей данных. Подсчитайте количество данных. |
N
|
N=36
|
| Диапазон
(R) набора данных - это наименьшая (минимальная) единица данных
минус наибольшая (максимальная) единица данных
|
R=max-min
|
N=76-60=16
|
| Класс
(К) используется для подсчета количества полос. Он равен квадратному
корню от N. |
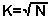
|
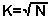
E=6
|
| Ширина
класса (H) используется для подсчет аширины полос. Она подсчитывается
делением диапазона на класс. |
H=R/K
|
H=16/6
H=2.6
округленно = 3
|
| Чтобы
начать построение гистограммы, установите начальную точку для
первого класса. Она подсчитывается вычитанием из минимальной
единицы данных одного измерения, поделенного на 2. |
Единица измерения (М)
М=1
min=M/2
|
60-1/2=59.5
|
| Теперь,
когда установлено ограничение для первого класса, постройте
таблицу частотности с тремя колонками. |
|
| Границы
класса |
Опознава-
тельный
ярлык |
Частот-
ность
|
| |
|
|
| |
|
|
|
| Чтобы
заполнить первую колонку, прибавьте к начальной точке класса
ширину класса (H) |
59.5+М
|
59.5+3
ширина
класса -
59.5
– 62.5
62.5
– 65.5, и т.д.
|
| Чтобы
заполнить вторую колонку, вернитесь к первоначальному набору
данных. Присвойте опознавательный ярлык тем данным, которые
попадают в границы каждого класса. Введите общую частотность
в третью колонку. |
|
| Границы
класса |
Опознава-
тельный
ярлык |
Частот-
ность |
| 59.5
– 62.5 |
|
3 |
| 62.5
– 65.5 |
|
6 |
| 65.5
– 68.5 |
|
6 |
| 68.5
– 71.5 |
|
9 |
|
71.5 – 74.5
|
|
8 |
| 74.5
– 77.5 |
|
4 |
|
Когда использовать гистограмму?
Гистограмму можно использовать
в этапе "Текущая ситуация", когда мы хотим получить точную
картину рассеивания или распространения данных.
Этап 3: Анализ
Цель - определить и убедиться
в истинности основных причин проблемы.
Ключевая деятельность
-
Выполните причинно
- следственный анализ проблемы.
-
Доведите анализ до
уровня действенных основных причин.
-
Выберите основные
причины, которые вызывают наибольшую отдачу.
-
Перепроверьте выбранные
основные причины данными.
Полезные приемы / средства
-
Причинно-следственный
анализ
-
Диаграмма Ишикава
-
Проверочный лист
-
Гистограмма
-
Диаграмма Парето
-
Контрольная диаграмма
-
График
-
Точечная диаграмма
Примеры:
|
Диаграмма Ишикава
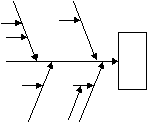
|
Диаграмма Парето

|
Точечная диаграмма
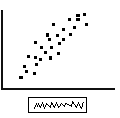
|
<
Предыдущий
| К
оглавлению
| Следующий
>
